FAQs numbers 10 toc19

10. How do I use calculated values from FCN or STATS in the HOME view?

For example, you wish to find the intersection of F1(X)=1/X and F2(X)=LOG(X) as accurately as possible and then use this in a calculation. Enter the two functions into the SYMB view, change to PLOT SETUP and press SHIFT CLEAR to reset to the default axes and then press PLOT. On the resulting graph, move the cross-hair to a point near the intersection and then use the FCN menu to find the intersection. The value quoted at the bottom of the screen is accurate to 7 dec. places.

Now, without doing anything else, change back to the HOME view and type X and press ENTER. The value which appears is the stored x coordinate of the last intersection point found. To find the y coordinate, evaluate F1(X) (or F2(X) - for that point the values are the same). This value can be used in calculations in the HOME view (such as 3*F1(X)+1 or LN(X)).

If you've found a Root or Extremum then you can do the same thing. If you've just used the FCN menu to find a Slope or Signed Area then you can also retrieve these but the method is a little more involved. Just use the A..Z button to type AREA or SLOPE and hit Enter.

Other values similar to these are stored in the Statistics aplet for you to use. Try this: go the APLET view, START the Statistics aplet, set it to 1VAR and enter a set of data into column C1. Make sure that SYMB is set with C1 ticked. Press the STATS button so that the univariate statistics are displayed. Now change back to the HOME view and press the VARS button. At the bottom of the screen you will see that is ‘ticked’ and that next to it is . Press and move the highlight down to ‘Stat-One’ and ‘Stat-Two’. These contain the list of calculated stats variables. For example, if you move to the right into the ‘Stat-One’ menu you will find all the variables listed in the STATS info screen seen earlier. These can be transferred to the HOME view and used in calculations. Just highlight them and press OK. The name appears in the HOME view and pressing Enter retrieves the value.

Note that what you see when you press the button depends on which aplet is active.

WARNING: The values stored are those of the last calculation done. If you have more than one column ticked in the SYMB view, resulting in multiple columns in the STATS display then the stored values will be for the last column only. If you wanted to calculate (for example) the mean plus 1.5 standard deviations for 3 different sets of data then you should use the VAR key to enter Mean+1.5*PSDev (Mean has a 'sigma' symbol after it which I can't show on this web page) into the HOME view and evaluate it for the first set of data. Then go back to the Statistics aplet and calculate the STATS for the next set and repeat. (The values are not stored in the VARs until you press STATS.)

11. How can I save my Notes?

Since Western Australia does not force students to reset the calculators before tests and exams, many students are creating elaborate collections of "cheat notes" in the Note view. Understandably, they get a bit worried that the batteries will fail and cause them to lose all their work.

If you go to my Utilities page you'll find a software package you can download that lets you send and receive notes, programs and aplets from the calculator to the PC and back. Windows only, I'm afraid! Any view which has SEND and RECV buttons can send either to a computer or to another calculator. You need the cable that came with your calculator - if you've lost it then just go to any electronics shop and ask for a mini-USB cable. They cost about $10 - $20.

See my Help page for a series of instructional pages on what hardware you need, what software and how to install it, and then how to use it all and where to look for aplets. You'll also find pages on programming the calculator which include screen shots.

12. How can I save a copy of an aplet?

This question is more likely to be asked by a teacher because the answer is really useful to them. Suppose that you have set up the Function aplet with a whole set of equations and set the axes in PLOT SETUP to exactly the appearance that you want. It would be nice if you could transfer this straight to the students' calculators, rather than waiting while they do all this on theirs. Alternatively you might have entered a large set of data into the Statistics aplet for use in a stats lesson and not want to waste time asking the students to re-enter it.

Just set up the aplet (whichever it is) exactly the way you want it, change into the APLET view and then, while it is highlighted, press SAVE. Give it a name and press ENTER.

The aplet can easily now be transferred to the students' calculators via the infra-red link. Once the class becomes used to this procedure it takes about 2 - 4 minutes for a class of 25 to 30. You send to one student, then the two of you send to two more, then the four of you send to... etc.

You can also save your aplet to a PC if you install the software (see my Utilities page). This means that you can re-use it next year!

13. When I find a solution in the Solve aplet, how do I use it in the HOME view?

This is a really easy one! Suppose you have an equation D=0.5*A*T^2 entered into the SYMB view of the Solve aplet. You have changed into the NUM view and entered the values of 50 and 9.8 for D and A respectively. You now move to T and press SOLVE and get the answer of 3.194382825 for T (ie. the time needed to fall 50 metres under standard gravity is 3.19 seconds).

Any of those values are now accessible in the HOME view by simply typing the appropriate letter. For example if you change to the HOME view and type T and hit ENTER, you will get the value I quoted above. If you type 3T+2, then you'll get 3 times the value of T plus 2. You can also use this in reverse. If you have done a calculation in the HOME view and you want to use it as the value of one of the variables in an equation in Solve, then just it into the appropriate memory and it will be pre-loaded when you enter the NUM view in Solve.

14. How can I get exact trig values on my calculator (ie. fractions of pi)?

This is a bit involved, but it does work nicely once you get the hang of it. It's a bit questionable really whether it's easier to do it by hand! As an example, we'll use the Solve aplet to solve for x in the equation 2sin(x)+2=1on the domain of 0 to 2pi. NOTE: In all the explanations following, I will use 'pi' to represent the proper symbol found on the 3 key.

In the Solve aplet, enter the equation 2*SIN(X)+2=1 in to the SYMB view. Change to PLOT SETUP and set the XRng to 0 to 2pi (using the 3 key to enter pi) and the YRng to -3.1 to 3.2. Enter an XTICK value of pi/4. Now press PLOT. Move the cross-hair close to the first solution (at about X=3.6) and then press NUM. If you now press SOLVE, the calculator will find the nearest solution of 3.665...

Change to the MODES screen and set the NUMBER FORMAT to 'Fraction 6'. Now change to the HOME view and type in X/pi. The answer is 7/6, so the required value is 7pi over 6. Basically you are removing the pi from the answer and giving the calculator the chance to tell you what the associated fraction was.

Now press PLOT, move near the other solution, press NUM and SOLVE, change back to HOME and press ENTER (to repeat the last calculation). This time the solution is 11 pi on 6.

The same method can be used in the Function aplet to find the exact value of intersections. Simply retrieve the value of the last intersection in HOME by typing X in the HOME view and use the same method to isolate the fraction.

Warning! Don't forget to change out of Fraction mode when you finish! If you have put the calculator into Fraction mode then it is going to give you a fractional answer even if the value you gave it was never meant to be one! If you get a fraction like 113/457 then you might suspect that there is a problem. See "How does the Fraction mode work?"

15. How does the Fraction mode work?

This is a really interesting facility but can easily turn and bite you if you don't understand it. Many of the calculators on the market have fraction buttons which allow you to add, subtract, multiply and divide fractions but the drawback of all of them is that many operations convert the fraction to a decimal. Generally once you do that there's no way to convert back. The HP will convert any decimal to a fraction.

Try this. Use MODES to change into 'Fraction 4' mode. Now go into HOME and type 0.33 and ENTER. You should find that it converts 0.33 into 33/100. Now try the same with 0.333333 This time you will find that it gives you 1/3. Why the difference?

The makers of the calculator have taken a very different approach. Once you select Fraction mode, all numbers become fractions - even decimals. If you are only going to be using fractions from that point on, then this will not cause a problem as long as you bear the following two points in mind….

The first point is that there seems to be no provision for inputting mixed fractions such as 3¹/₄. Fractions are entered using the divide key / and, while the calculator is quite happy with improper fractions such as 5/3, it (correctly) interprets 1/2/3 as (1/2)/3 (one half divided by 3) and gives a result of 1/6 ! The solution to this problem is simply to enter mixed fractions as (1+2/3). While the brackets are often not strictly necessary it is a good idea to include them anyway or "Order of Operations" problems may occur, such as 1²/₃*¹/₅ being interpreted as 1+(2/3*1/5) rather than as (1+2/3)*1/5.
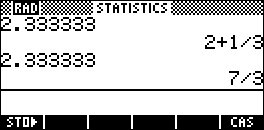
You can, on the other hand, tell the calculator to output fractional results as a mixed fraction by setting the MODES screen to Mixed Fraction instead of Fraction. The difference of output can be seen in the screen capture shown right. If you COPY a result for use in a later calculation you must be careful to enclose it in brackets!
The second important point involves a characteristic of the approach taken by the calculator, and lies in the method used to convert decimals to fractions.
The method the calculator uses is basically to generate (internally and unseen by you) a series of continued fractions which are approximations to the decimal you typed in. The final fractional approximation chosen for use is the first one found which is ‘sufficiently close’ to the decimal. The trap lies in what constitutes ‘sufficiently close’, and this is determined by the ‘4’ in Fraction 4. Very roughly, the calculator will use the first fraction it finds in its process of approximation which matches the decimal to that number of significant digits. The process is actually more complex than this, but it will do for an approximation.

For example, a setting in the MODES view of....

'Fraction 1' changes 0.234 to ³/₁₃ which is actually 0.2307692… (matching to at least 1 sig. fig.)

'Fraction 2' changes 0.234 to ⁷/₃₀ which is actually 0.2333333… (matching to at least 2 sig. fig.)

'Fraction 3' changes 0.234 to ¹¹/₄₇ which is actually 0.2340425… (matching to at least 3 sig. fig.)

Fraction 4 changes 0.234 to ²³⁴/₁₀₀₀which is exactly 0.234 (matching 0.2340 to 4 sig. fig.)

Basically, the value of ‘n’ in ‘Fraction n’ affects the degree of precision used in converting the decimal to a fraction. This can be useful if you understand what is happening. For example, a setting of Fraction 4 produces a strange (but actually fairly accurate) result for 0.667, while changing to a setting of Fraction 2 will give a result of 2/3. In other words, what makes this approach taken by the calculator useful is that it is often capable of producing results which may be strictly less accurate but are probably closer to what was intended by the 0.667 in the first place.

If you are wanting to use this facility to convert decimals to fractions, here are some tips…

if you are converting a recurring decimal, ensure that you include more decimal places in the number you enter than your Fraction setting. For example, in Fraction 4, enter 0.33333 to get 1/3. Not including enough decimal places does not produce good results as you can see with the earlier example of 0.234

if you are converting an exact decimal to a fraction, then set to a Fraction value more than the number of decimal places in the value entered. For example 0.125 becomes 1/8 in Fraction 4.

Forgetting the current setting of Fraction can produce some unfortunate effects. For example, at Fraction 2, the value of 123.456 becomes 123, with the 0.456 dropped entirely!

This need for a correct setting of Fraction extends even to working purely with fractions. For example a setting of 'Fraction 4' will correctly result in 1/3 + 4/5 = 17/15. If you use a setting of only Fraction 2 to perform this, you will find to your amazement that 1/3 + 4/5 = 8/7 ! The reason is that the 1/3 and 4/5 were converted to decimals and added to give 1.133333…. This was converted back to a fraction (needing to match only to 2 sig. fig.) to give 8/7 (which is 1.1428..).

In conclusion, while it is not at all suggested that you dismiss the use of the Fraction format, it is important that you understand and remember its limitations. See an earlier question regarding using fraction mode for exact trig values.

16. My batteries sometimes seem to run out very quickly

Any activity involving communications, either via the cable or via the infra-red link, will use up the batteries more quickly. Consequently if you are transferring a lot of Notes or Aplets then you may find that they don't last as long. Similarly you'll find that if you're having problems with communication with your PC then it's most often due to low batteries - even if the 'low battery' indicator has not yet lit up.

17. Why does the square root of negative 9 give an answer instead of an error?

In lower school mathematics we are taught that the square root of a negative number does not exist. In fact, it does exist - it just isn't a 'real' number. There is a whole branch of mathematics concerned with what are called 'imaginary' or 'complex' numbers and the calculator is designed to allow their use because they are part of some of the upper school courses. You can recognise a complex number by the way the calculator writes it - as (0,3) or (2.13,-1.7). Any time that you see an answer written in brackets it means that the number is complex.

This affects the POLYROOT function too. If you use POLYROOT to solve the quadratic equation of x^2+4x+5=0, which does not cross the x axis (try graphing it!) you will find that it gives the roots as complex numbers. They are NOT (x,y) points on the x, y axes! Don't use them - just write "No real solution".

ie.POLYROOT([1,4,5]) gives [(-2,1),(-2,-1)]

Another similar problem is with the inverse trig functions. Since sine and cosine have ranges of -1 to 1, there should be no answer to ASIN(1.2). However, the calculator will return a complex answer.

18. Why the jaggy lines in graphing (1+1/X)^X for an extreme range?

The question: I am a year 11 student in Western Australia and I am having a problem with the HP. I am having trouble graphing a function & was wondering if you could help. The function is (1+(1/X))^X, changing the 1/X to certain figures eg. (1+(2/X))^X Upon graphing for the XRng 0 to 1E11, the function line obtained is a zig-zag kind of line. In fact the graph is supposed to be smooth. I believe the calculator rounds the digits or something like that.
Sam McHarg (Denmark SHS, W.A.)

The problem is caused by the internal rounding of the calculator. It works internally to 16 bits, which means that it can store 12 significant digits (for reasons only of interest to programmers). This means that when you invert a really large number and add it to one, you lose a lot of accuracy. For example: if X = 2.85E10 then 1/X is 2.5087719298E-11 However, when you add 1 to this, the calculator is forced to discard all but the last decimal place. Thus 1 + 1/X = 1.00000000003 (rounded off from 1.00000000002508...)	Expected result (0 to 100)
There are naturally a whole range of numbers which will all round off to the same value of 1.00000000003, so that (for that range of numbers) the expression (1+1/X)^X is equivalent mathematically (on the HP) to (1.00000000003)^X. This produces a short section of an exponential graph, which only looks linear because you don't see enough of it.	Starting to be unstable (0 to 1E11)
Eventually the calculator reaches a value on the x axis which is large enough that it rounds off to a smaller number than 1.00000000003, which is 1.00000000002 This produces the sudden drop in the graph as the plot changes from a section of a 1.00000000003^X graph to a section of a 1.00000000002^X graph (which has a shallower gradient). This section is maintained then until the next drop, and so on.	The real problem... (0 to 1E11)
Finally the value of X becomes so large that 1 + 1/X cannot be distinguished from 1 to the calculator's accuracy. At that point the expression (1 + 1/X)^X becomes equivalent to 1^X, which is simply a horizontal line of F(X)=1. If you change the scale from XRng 0 to 1E11 to an XRng of 0 to 4E11 you will see this happen. The point of change is when 1/X becomes less than 1E-12 when rounded, which is at X=2E11.	The final stages (0 to 2E11)

See also, a detailed paper on teaching Calculus concepts using the HP. This includes further information on problems with limits.

19. How can I quickly clear the memory on the calculator completely?

The easiest way is to do a 're-boot' or hard reset. This is done by holding down the ON button and, while still holding it down, pressing & holding the first and last of the screen buttons. Wait about a second and then release the buttons in the opposite order. On the HP38G it doesn't matter if you don't get the order of release right but on later models (39G/40G/39g+/39gs/40gs) it does matter. You have to release SK6 first, then SK1, then ON. If you've done it right you should see a message telling you that the memory has been cleared. If you get the order wrong then it may go into diagnostic mode with all sorts of garbage appearing on the screen. Press ON+SK3 to stop this.

Note: The ON+SK3 is a less drastic version called a soft reset which only does a 'memory sweep' rather than a complete memory clear.