FUNCTION PLUS and WindFix
This is either an aplet or a program, depending on how much memory you want to use up. As an aplet it is an enhanced version of the Function aplet with one extra option in the VIEWS menu of 'Window Fix'. As a simple program called WindFix you need to change to the Program Catalogue to RUN it but it saves the memory overhead of storing an entire aplet.Running the program or choosing this new option will cause the values of Xmin, Xmax and Xtick for the PLOT veiw to be redefined to 'nice' values instead of the usual horrible decimals that you get if you choose a convenient scale like -10 to 10. These horrible values are caused by the scale failing to match the number of pixels on the screen.
The user is presented with the choice of 'Decimal screen', 'Trig. (Radians)', 'Information' or 'Cancel'. Choosing 'Decimal screen' will make the aplet look for the nearest (larger) scale that will give nice jump sizes when using Trace. Nice scales are ones that use 0.1, 0.2, 0.25, 0.4 or 0.5 (or the equivalents in powers of ten of these, such as 10 or 0.0025 etc.) The screen is also moved if necessary so that zero falls on a nice point.
Choosing the 'Trig. (Radians)' will cause the scale to be adjusted so that the cursor jumps by 'nice' fractions of pi. Fractions used are pi/54, pi/48, pi/36, pi/24, pi/18or pi/12.
NOTE: If you download only the program, you need to download it into the
Program Catalogue NOT the Aplet Library. The desintation is different but the
procedure is the same.
.
.
.
GP SOLVER
This is a copy of the Solve Aplet with the three equations used in dealing with Geometric Progressions pre-entered. It can be used to solve problems in geometric sequences and series quickly and easily.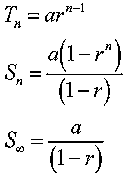
My students found it really useful. I suspect it will be one of those ones
that proves very difficult to get them to erase.
.
.
.
LINEAR PROGRAMMING
This aplet will solve
linear optimization problems for any number of linear constraints.
.
It will graph the
feasible region, give the coordinates of all intersections of the region and
evaluate the objective function to find the maximum and minimum possible values
in the feasible region.
.
.
.
