The Wow Factor

by Colin Croft

Note: This page is adapted from an article which appeared (much edited!) in the September, 1998 issue of HPc (Hewlett Packard's magazine for users of the 38G and 48).

The place:

A hotel room in Perth, Western Australia in early March, 1998.

The assignment:

Produce a set of ideas for ApLets which will cause the average mathematics teacher to say "Wow!". Implement them in time to be demonstrated at the NCTM conference in April.

The result...

Using the ideas which were mapped out during that weekend, two HP programming gurus and I teamed up to write two ApLets called "Quadratic Explorer" and "Trig Explorer". I'm hoping that these may prove to be the first of a series of new ApLets.

Both of these first two ApLets were inspired by the 'Active Grapher' aplet which many teachers have already found useful.

So, with due thanks to Gerald Squelart and Jean-Yves Avenard for their expertise with machine code, I hope you'll enjoy being 'wowed'...

The Quadratic Explorer aplet

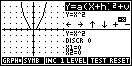In line with the philosophy of encouraging the student to take control of their own learning, this aplet lets the student investigate quadratic graphs by manipulating the graph and the equation. A worksheet is supplied with the aplet which encourages the student to make observations about the behaviour of the graph, recording their conclusions as they go.

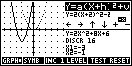Since it is written in machine code, this aplet is blindingly fast and does not have the normal SYMB, PLOT and NUM views. When the user STARTs the aplet they will see a screen split to show the basic y=x2 graph, together with information on the roots and the discriminant. As the graph is modified, this basic graph is retained in dotted form for comparison.

The view you see left is the GRPH view, so named because the user has control of the graph.
.
.
Using the arrow keys the user can move the graph around on the screen, while the plus [+] button, the minus [-] button and the sign [-x] button can be used to change the gradient. These changes happen extremely quickly and are immediately reflected in the equation shown on the screen on the right. The equation is quoted in graphical form and in parametric form with redundant coefficients removed.

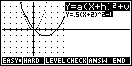
Highlighted at the top of the right hand screen you will see Y=a(X+h)2+v. Since the teacher may want the student to investigate only one coefficient at a time, the LEVEL button allows the user to set either 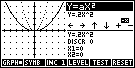Y=aX2, Y=(X+h)2, Y=X2+v or all three at once as Y=a(X+h)2+v.
.
.
.
.
.
The screen is set to display the range -5 to 5 on both axes but this changes (instantly!) as the graph moves off the edge of the screen.

The size of the movement can also be controlled via the INC button, allowing values of 0.5, 1 or 2.

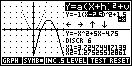So far we have used GRPH mode to see changes in the graph reflected in the equation. You may prefer that the student investigate the quadratic's behaviour by seeing changes in the coefficients reflected in the graph. In that case, simply press the SYMB button to change to SYMB mode (the normal PLOT and SYMB buttons can be used also).

In this mode the left/right arrows move between coefficients, while the up/down arrows change them. The range of possible values is not infinite but will certainly allow full exploration of the graph's behaviour. For example, whether the user is in GRPH mode or SYMB mode the values of the 'a' coefficient are restricted to the values of ±0.1, ±0.2, ±0.3, ±0.5, ±1, ±2 and ±5. Restricting these values was Gerald's choice and is a major factor in the incredible speed with which the graph is drawn on the screen.

Once exploration is concluded, the student's understanding of the graph's behaviour can be evaluated using the TEST button. Pressing TEST will generate a random graph for which the student must find the equation. EASY graphs are ones which remain within the range -3 to 3, while harder 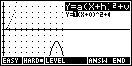graphs can use the full screen of -10 to 10. The LEVEL button is also available in this view.
.
..
The student now uses the arrow keys to adjust the coefficients until they feel that the equation matches the graph. As soon as the student alters the equation in any way another button labelled CHECK appears. If the equation is not corrrect then pressing this button will create an 'animation' where the display flashes back and forth between their suggested graph and the one whose equation is being sought. This gives immediate feedback on exactly how their answer differs from the required one.

To fully appreciate how effective this animation is you will have to download the aplet and try it for yourself - talking about it just doesn't do it justice!

The student can of course give up at any time by pressing the ANSW button. The number of attempts made before successfully finding the equation is tracked and reported by the CHECK button.

A worksheet is supplied with the aplet which is written to allow guided exploration independent of the teacher. The student is required to record their observations and conjectures at each stage and then to report in writing on their final conclusions.

The Trig Explorer aplet

Despite the fact that the sine and cosine graphs are amongst the most interesting to explore and to graph, many teachers are reluctant when it comes time to teach them because of the amount of time needed to draw the graphs. My answer to this has always been to use a computer package but unless you are fortunate enough to have access to a multitude of computers this means that the lesson tends to be teacher driven rather than a student oriented discovery lesson.

The Trig Explorer aplet is very similar in behaviour to the Quadratic Explorer. The aim of the aplet is for the student to investigate the effects of the coefficients of a, b, c and d on the graph of Y=a sin(bX+c) + d.

This aplet again gives the user the option of having the graph control the equation (in GRPH mode) or the equation control the graph (in SYMB mode). The original graph will again stay visible for comparison.

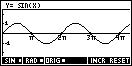The user can swap from sine to cosine or from radians to degrees using the buttons provided on the screen. The scale automatically changes from degrees to radians as the user does this. Values of the phase shift are given as a multiple of p when in radian mode.

The INC button controls the size of the step used when moving horizontally.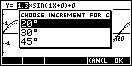

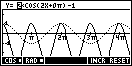When in SYMB mode the left/right arrows move from one coefficient to the next, while the up/down arrows change them.

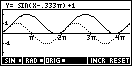
In GRPH mode the control method is slightly different. There are two points of control, called the origin (ORIG) and extremum (EXTR). These points of control are shown above.

When the control point is on the ORIGin then the arrow keys affect the phase and vertical translation. When it is moved to the EXTRemum then the arrow keys affect the amplitude and frequency.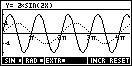

Holding down the arrow keys produces an effect which I would dearly love to be able to show since it is a credit to Jean-Yves programming skills. He has managed to redraw the graph on the screen so rapidly that it actually appears to visibly crawl as the coefficients change! Since even HP have not yet managed to embed animated graphic files into the hpc magazine you will have to wait until you download the aplet to see this in action. If you can watch the animation of the frequency change without a quiet "Wow!" then please have someone push you over and throw dirt on you - your sense of wonder is already dead!

Since the students who are to be investigating trigonometric graphs are usually mathematically more advanced, the worksheet which is provided with this aplet is less guided than the one which comes with the Quadratic Explorer aplet. It focuses on encouraging the students to make observations, form hypotheses, and then to test and revise them.

About the authors of the ApLets...
Apart from me, Gerald and Jean-Yves are former free-lance HP48 programmers who are now employed by HP to work on 38G (and still also on 48 stuff) in Melbourne, Australia. The originators of the project were Charles Lim, who is also based in Melbourne, and Bob Parker, based in Perth.