Misc
Home Help FAQ Page Aplets Games Utilities Web Links What's New? Contact Me

 

Bisection 
Although bisection is no longer used as a method of finding roots of equations since graphical calculators became available, it is still often taught in schools. This aplet may help you to understand the process.

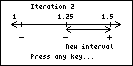
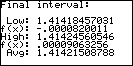
The program assumes the equation is in F1(X) of the Function aplet.  Given initial upper and lower bounds within which a root lies, and the degree of accuracy desired for the solution (number of decimal places), this program will visually show the progressive narrowing of the bounds in search of a solution.
Note: This is one instance in which the program is different for a 38G user than for a 39/40G user, due to some extra programming commands which are available in the new machine. The display shown right is for a 39/40G and the 38G display is less graphical.

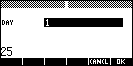
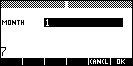
Day of Week 
Given a date (day, month, year), this program will tell you the day of the week. The result is given as a number.
It should be noted that there were a number of serious calendar reforms during the past centuries which will make the results inaccurate in the case of finding (for example) a date in the 17th century.

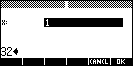
Log a base b 
If you are not comfortable with the change of base law in logarithms, this program will give you the log of any number to any base.


N-R Table 
This program assumes that the function has been placed into F1(X) of the Function aplet and then uses the Newton-Raphson iterative method of xn+1=xn - f(xn)/f '(xn) to find the required root to the degree of accuracy specified, showing all working in the process.

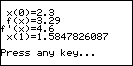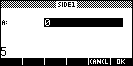
Pythagoras 
Uses Pythaoras' rule to find the length of the hypotenuse or one of the other two sides in a right triangle.

Rule Finder 
This program searches for a rule connecting columns C1 and C2 of the Statistics aplet.
Note: In this case (as shown right), the data in column C2 has been manufactured in the HOME view for each of the two examples below.
The program checks for a linear rule of the form y=mx+c, a quadratic rule of the form y=ax2+bx+c, an exponential rule of the form y=a*bx or a power rule of the form y=axn.
Due to the fact that the values in C2 may be rounded off (particularly in the case of an exponential rule) there is a certain amount of built-in slack that will allow the program to suggest a rule even if the numbers in C2 don't match the rule exactly. In this case it will mention at the end of the program that it has done this.

For example, an exponential rule that has a rule of (say) y=35*1.03x might be reported by the program as being linear because the values are so close to a straight line.

Note:  The program uses the powers of the Statistics aplet to perform its search for a rule and the user may find that settings in this aplet will be disturbed by the program.

38G Memory
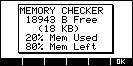
This program will display the amount of remaining memory on a 38G.  This is not required for a 39/40G since you can just press the MEMORY button to perform the same function in greater detail.
Note: This program must NOT be run on a 39/40G. It will reset the calculator, causing all programs and data to be lost (but will not otherwise damage it). The version in the 39/40G collection is just a dummy that prints a message to that effect.

Last modified: 19 Dec 2007                                             Sitemap        Home        Contact Me