| |
| |
. .
|
Central
Limits Theorem |
| |
One of the most fundamental theorems in the study of
statistical inference is the Central Limits Theorem. This states
basically that the means of successive random samples taken from
a population will be normally distributed whatever the
underlying parent distribution.
This aplet illustrates this and that the standard deviations are
related by ratio. Sampling can be done from different parent
distributions and the resulting collection of means compared to
the equivalent Normal distribution. It is fairly slow to execute
because of the need for repeated sampling but would be quite
useful to teachers. |
|
 |
|
 |
|
| |
.
|
Correlation |
| |
This small but handy aplet created by David Kranz allows you
to find the correlation and line of best fit from summary
statistics. Only the 39/40G version is available and this is not
likely to change. |
|
 |
|
|
|
| |
. .
|
First 50, The |
| |
This is a collection of small programs you can type in
yourself or download. They perform a multitude of small
tasks, some that are so easy you'll wonder why I wrote a program
for them, some that are really cool. For FAR more information click
here.
Author: Colin Croft
|
|
|
|
|
|
| |
. .
|
Grouped Data |
| |
This aplet calculates and displays measures of central
tendency and spread for data which has been grouped into
intervals. The user puts the interval mid-points into C1, the
frequencies into C2 and the aplet will display the mean,
proportional median, lower and upper quartiles and various other
values. The user can also perform calculations such as finding
the values which cut off the top 15% of data, the middle 30%
etc.
Update (9May'04): Fixed a small
bug in the graph display.
Author: Colin Croft |
|
|
|
|
|
| |
.
|
Inference |
| |
This aplet gives inferential statistics access for the 38G
similarly to that of the 39/40G, covering both Hypothesis
Testing and Confidence Intervals. The interface is not as
smooth as the 39G version and there is no graphical view to aid
in your judgement but it does the trick extremely well and fills
a hole in the capabilities of the 38G. Documentation is
included. Many thanks to Detlef Muller for transforming it from
my HPBasic program that used 75% of memory on the calculator to
an assembly code aplet that uses only 23%!
Note: See also Statpack 39/40.
Updated (7/1/05): Fixed a small bug that gave an error in
one of the calculations. Spotted by Fabio Frascati. Thanks to
Detlef for revisiting the code so long after he wrote it.
Author: Colin Croft, Detlef Mueller. For source code
click here.
|
|
|
|
 |
|
| |
.
|
Key Finder |
| |
This aplet uses a statistical model to simulate a person
trying to find one particular key of six in their pocket. A
investigation into the average run length when throwing dice.
More Information
Author: Colin Croft
|
|
|
|
|
|
| |
.
| KeyDebounce |
| |
The internal keybounce time is set in order to prevent a key
registering twice. When you press a key you may only hold
it down for a fraction of a second but to the calculator this is
a LONG time and if there were no delay set then it might, for
example, read what you meant to be a '3' as a '33'.
However the default factory setting of 166.6ms delay is a little
high and sometimes causes a REAL press of '33' to only register
as a single '3' when you actually meant 33! Changing the
delay value to a setting of around 75ms will reduce the chance
of this happening.
When you first run the aplet it will display the current
delay time. For an HP39G this is 166.6 milliseconds.
You can alter this to any value from 0 to 400. Based on my
experience a good value to try is somewhere around 100ms.
Once the value is set it will remain until a memory reset
(ON+SK3 or ON+SK1+SK6) is performed on the calculator. Deleting
the aplet will not affect it and, since the aplet is only 1.3Kb
in size, it may be worth retaining.
Note: This aplet was written
for the old 39G/40G that have since been superseded by the
39gs/40gs. It makes calls directly to the chip and may not work
for the 39gs. It may have no effect or it may even lock up the
calculator, requiring a reset!. I've not tested it. Feedback
would be appreciated.
Author: Detlef Mueller
|
|
|
|
| |
. .
| Maths & Chem Library |
| |
This aplet allows the 39g to execute a number of new commands
for use in the Western Australian TEE subjects Calculus,
Chemistry and Applicable Maths. It contains a number of small
routines for use in exams. To use the commands, simply type the
desired command in the home screen as you would an inbuilt
command. Most of them can also be done using the Solve aplet but
this is faster.
====COMMANDS====
* BIN(x,n,p) - finds the binomial probability of X=x
* CBIN(x,n,p) - finds the binomial probability of a=X=b
* POI(x,µ) - finds the Poisson probability of X=x
* CPOI(a,b,µ) - finds the Poisson probability of a=X=b
* EXPON(a,b,µ) - finds the exponential probability of a=X=b
* CIS(n) - performs the complex operation CIS on any angle
To find the atomic mass of any element, type the atomic formula
(eg He for helium) followed by a full stop, and press enter.
Author: Alan Lark |
|
|
|
| |
.
| Probability Distributions (Updated!) |
| |
An essential tool for any student going into an exam which
involves probability functions. This is two copies of the Solve
aplet with equations pre-entered for Discrete and Continuous
probability density functions respectively. Covers the Binomial
distribution (individual & cumulative), the Poisson
distribution (individual & cumulative), the Exponential
function, the Normal distribution, plus more. Make sure
you read the documentation.
Note: Updated 19/4/03 to split it
into Discrete and Continous PDFs.
Prior to that
all equations were in one aplet.
Updated 30/8/04 to fix an error in the documentation.
Updated 11/9/05 to fix another error in the documentation.
Author: Colin Croft, Craig Davis & various students. |
|
|
|
|
|
| |
. .
| Serpinski |
| |
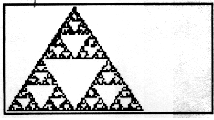 This
aplet illustrates the chaotic production of Serpinski's Triangle
by random processes which nevertheless produce a deterministic
result.
Author: Detlef Mueller
|
|
|
|
| |
.
| Simulations |
| |
This aplet allows the teacher to simulate sets of observations
on a multitude of discrete and continuous probability
distributions for use in tests and exams. It will probably not
be of interest to students.
More Information
Note: Updated (9/12/00). The zip file was not
extracting properly. No change to the aplet itself.
Note: Updated (27/8/04). Added the ability to simulate the
Poisson distribution.
Author: Colin Croft
|
|
|
|
|
|
| |
.
|
Statpack39/40 |
| |
This is an incredibly useful package for advanced stats
developed by Tim Wessman in the US. It massively enhances
the statistical capabilities of the HP39G or the HP40G with a
number of new functions. An absolute must for any university
mathematics students. An HP38G version is not available
and is not likely to be.
Click here to view the
documentation in PDF format, or click on the link on the right
to download the whole package (118Kb).
Note: The author is currently out of touch and will not be
available until 2004. Any bugs or problems should be
reported to me and I will pass them on later. I have the
source code if any machine code programmer is interested in
doing maintenance. You'd need experience in using sRPL on the
HP48 or HP49.
Author: Tim Wessman
|
|
|
|
| |
. |
|
| |
|
This aplet contains sets of bivariate data which have the same
summary statistics but totally different 'shapes' when graphed.
They illustrate the need to rely on more than just the stats
when deciding on whether a linear model is appropriate!
Highly recommended. This aplet
investigates the common charity game consisting of tossing of a
coin onto a square grid. It requires only knowledge of
quadratic functions and can be used at a number of levels:
This aplet uses visual methods to illustrate and introduce the
Poisson distribution, through the sowing of dandelion seeds into
a large patch of ground, which is then broken up into unit
squares.
Using
the Fisher Z Transform aplet, the student will be able to
perform standard calculations involving Hypothesis Test and
Confidence Interval about ρ (correlation coefficient).
The student nominates what they think is the line of best fit
for a set of bivariate data. They can then adjust the line
interactively, seeing the effect on the sum of squares of
residuals. The HP38G version is an effective teaching tool
even if a bit slow but new commands available on the HP39G have
let me speed that version up considerably.
This
is an aplet created by Fabio Frascati. It is quite similar to
the Probability Distributions aplet above except that it deals
with more advanced probability functions and that it has been
automated via the VIEWS menu. Well worth downloading for any
student using this level of statistics.
This aplet performs time series analysis using any length
moving averages from 2 to 8 points. It includes extensive
graphing facilities and the ability to produce seasonally
adjusted data.