The Loan Table Aplet
This is one of those "must have" aplets for students who solve problems involving borrowing money and making regular repayments.
Once you have it on your calculator all you have to do is store the amount borrowed into P, the interest rate in to R and the amount being repaid into A in the HOME view and the aplet will then show you the remaining principal and interest charged each year/month/quarter.
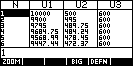The nice thing is that you don't need a cable for this one - it is quite easy
to set up, although you'll have to be careful to enter the equations correctly.
The example shown is $10000 at 5% pa with $600 repaid. Click on the link to the
left for instructions on how to set it up, or go to the Misc Aplets page to download the aplet ready made.
To set up the aplet just SAVE a copy of the Sequence aplet and then enter the equations below into the first three sequences. U1 gives the amount owing, U2 the interest for that period and U3 the repayment.
U1(1)=P
U1(2)=ROUND(P*(1+R)-A,2)
U1(N)=U1(N-1)+U2(N-1)-U3(N-1)
U2(1)=ROUND(P*R,2)
U2(2)=ROUND((P*(1+R)-A)*R,2)
U2(3)=ROUND(U1(N)*R,2)
U3(1)=A
U3(2)=A
U3(N)=MIN(A,U1(N)+U2(N))
All you need to do now is to enter the values for P, R and A that you need for your problem.
Note: These equations may seem a little complicated but the reason for this is to ensure that a) all amounts are give to 2 decimal placed, b) the amounts never go negative, and c) the final payment made on the loan is the smaller of the amount owing or the regular repayment. Otherwise your last payment would be more than you owe and you'd continue to pay long after the amount owed went negative! If you'd rather work with equations that are easier to understand then use the ones below. The ones above are MUCH better though!
U1(1)=P
U1(2)=P*(1+R)-A
U1(N)=U1(N-1)+U2(N-1)-U3(N-1)
U2(1)=P*R
U2(2)=(P*(1+R)-A)*R
U2(3)=U1(N)*R
U3(1)=A
U3(2)=A
U3(N)=A
eg.
Find the amount owing at the end of the first year, the total time to repay the
loan and the final repayment, if I borrow $10,000 at 18% pa with monthly
repayments of $200 per month.
As can be seen to the right, just use the HOME view to enter the
values of 10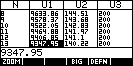
,000
into P, 0.18/12 into R (the monthly rate) and 200 into A.
Then swap to the NUM view and scroll down to N=13 to find that the
amount owing at the end of the 12th month of $9347.95
To find the term of the loan, make a guess and enter that value into the N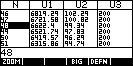
column. For
example, guess N=48 (4 yrs) and you'll see the result shown right. Note
that you will find that recalculating the values will take a few seconds due to
the complexity of the formulae. Clearly this is too soon!
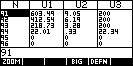Some
experimenting will result in a screen like the one to the right. This gives the
total time as 94 months (7 yrs 10 months) and the final repayment as $22.34.