| |
| |
.
.
..
| Complete the Square |
| |
This is a simple program written by a student which takes a
quadratic in the form y = ax2+bx+c and converts it to
y=a(x+h)2+v form. Because it is a program it should be
downloaded into the Program Catalog.
Author: Grey Johnston |
|
 |
|
| |
.
| Complex Roots |
| |
This shows the nth roots of a complex number on an argand
diagram and gives their values in the forms a+bi and r
cis theta. This is a small program rather than an
aplet and must be downloaded to the Program Catalog not to the
Aplet Library.
Author: Andy Vella, Colin Croft |
|
 |
|
|
|
| |
.
.
| Curves Collection |
| |
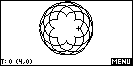 This collection of mathematical curves was
originally hosted on Jim Donnelly's page but has been shifted to
mine now that Jim has moved on to other interests. These apLets allow the user
to explore interesting mathematical curves. Includes Cardiods,
Catenaries, Astroids and Lissajous curves. Excellent fun!
Ideal for a maths enrichment class.
Author: Jim Donnelly
|
|
| |
.
| DFind/DSolve and QPrograms |
| |
DFind/DSolve: This paired set of aplets, based
around the Function and Solve aplets, allow the user to quickly
and easily find the features of functions such as intercepts and
extrema using derivitives, automatically finding the derivative
functions as part of the process. Obviously this is something
which can already be done with the Function aplet but these two
aplets automate the process by switching automatically between
the abilities of the Function and Solve aplets. As an
examination tool it is definitely worth having. Note:
When you unzip this aplet and transfer it to the
calculator you must be sure to download both aplets -
DFind
Updated: (24/3/02) A new version of
DFind/DSolve has been posted which runs more efficiently.
Updated: (7/4/02) Again another
newer version which has enhanced capabilities.
.
QPrograms: This is an aplet which lets you perform
a number of small tasks - calculate coefficients for binomial
expansions, calculate mean and standard deviation of grouped
data and divide complex numbers.
.
These aplets were created by Matt Grosvenor, who is (in 2002) a
final year student at Perth Modern School. Matt only
produced versions for the HP39G so HP38G users are out of luck
in this case.
Author: Matt Grosvenor
|
|
-----------
|
|
|
|
| |
.
.
| Function 'Plus' |
| |
This is a copy of the Function aplet with an extra entry on
the VIEWS menu which produces 'nice' scales. You may have
noticed that the default plot view scale of -6.5 to 6.5 produces
'nice' step sizes of 0.1 when using the trace facility.
This aplet will allow you to set whatever scale you choose and
then correct it to the closest approximation which will still
offer similar 'nice' trace values such as 0.2, 0.25, 2, 0.04
etc. It includes the ability to produce scales which are
'nice' fractions of pi for use with trig functions.
More Information
An alternative to this aplet is a program called Windfix (see
below). This program can be used with any aplet and takes up
less memory.
Author: Colin Croft
|
|
|
|
|
|
| |
.
| First 50, The |
| |
This is a collection of small programs you can type in
yourself or download. They perform a multitude of small
tasks, some that are so easy you'll wonder why I wrote a program
for them, some that are really cool. For FAR more information click here.
Author: Colin Croft
|
|
|
|
|
|
| |
.
.
| GP Solver |
| |
This aplet is simply a copy of the Solve aplet with the
relevent equations for geometric progressions pre-loaded.
You can set it up easily yourself if you want to.
More Information
Author: Colin Croft
|
|
|
|
|
|
| |
.
.
.
| KeyDebounce |
| |
The internal keybounce time is set in order to prevent a key
registering twice. When you press a key you may only hold
it down for a fraction of a second but to the calculator this is
a LONG time and if there were no delay set then it might, for
example, read what you meant to be a '3' as a '33'.
However the default factory setting of 166.6ms delay is a little
high and sometimes causes a REAL press of '33' to only register
as a single '3' when you actually meant 33! Changing the
delay value to a setting of around 75ms will reduce the chance
of this happening.
When you first run the aplet it will display the current
delay time. For an HP39G this is 166.6 milliseconds.
You can alter this to any value from 0 to 400. Based on my
experience a good value to try is somewhere around 100ms.
Once the value is set it will remain until a memory reset
(ON+SK3 or ON+SK1+SK6) is performed on the calculator. Deleting
the aplet will not affect it and, since the aplet is only 1.3Kb
in size, it may be worth retaining.
Author: Detlef Mueller
|
|
|
|
| |
..
| Library L1542 (Version 1) |
| |
Released 8th July, 2003. This is an upgrade to the L1540
Library which also incorporates string handling. You need this if you're a serious programmer!!
Note: The included documentation is good but
terse. I will be providing more detailed documentation when I have
time. Check back later.
L1542 is a 33KB SysRPL library for the HP39/40. When you download it to your calculator this library gives
access to an add-on collection of extra functions which then
become available in HOME, in programs or in the CAS (on an HP40G). The
functions essentially comprise much of what makes the difference between an
HP40 and an HP49, plus some more.
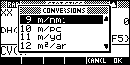
Functions added include a decimal/hex conversions, a calendar,
a list of metric/imperial conversions, a list of physical
constants, some time/value/money functions similar to those on the
TI89, probability functions, vector plot and matrix slope plot,
multidimensional optimisation, discrete Fourier transforms and
numerical solution of differential equations. Even a help
command is included which explains how to use each function!
For programmers there are REALLY useful functions that let you
do bit manipulations, perform graphic plots, call programs in
nifty ways as functions (ie. returning values), use local variables
instead of the global ones A..Z and, most importantly, input,
manipulate and output string variables. String constants can also be realized with
the aid of an additional tiny library L1840, which is included in this
package.
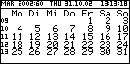
This library even has a command to delete itself so that you
don't have to reset your calculator (losing not only the library
but everything else as well).
The source is included and compiles with the HP DOS tools.
Author: Martin Lang (Germany), with contributions from Jordi
Hidalgo.
|
|
|
|
| |
..
.
| Linear Programming |
| |
This aplet visually solves linear programming problems,
finding the vertices of the feasible region and the max/min of
an objective function. The final stage of finding the vertices
is a very slow on an HP39G, but not too bad on a 39g+, and the result is very impressive.
In the latest version you can also do sensitivity analysis on
the solution you find. You can also edit constraints once they
are entered which makes it a wonderful
tool for teachers marking test papers - it lets you easily
check whether a student's feasible region is correct if they
have one or more of their constraints wrong. That's why I originally wrote it:
sheer frustration after the 20th paper that had to be reworked
from scratch to assign part marks. My students who
had HP38Gs decided that it was not one of the aplets they would
take into an exam because of its size but that won't matter on
an HP39G or hp 39g+ and the new ability to do sensitivity
analysis makes it essential.
More Information .
Note: Updated (6/8/99).
Instead of discarding existing data every time the aplet is run,
it now gives the option of retaining it. This means you
can exit the aplet, do something else and then re-run it without
losing your constraints.
Note: Updated (8/8/04). Added sensitivity analysis to the aplet
and the ability to edit constraints once entered.
This makes it an essential tool for any student. (The 38G
version was not updated.)
Note: Updated (16/8/04). Three small bugs fixed.
Note: Updated (20/8/05). Added the ability to delete constraints
from the list rather than only edit them.
Author: Colin Croft
|
|
|
|
|
|
|
| |
.
. .
| Root Finder |
| |
This is a program not an aplet and
must be downloaded into the Program Catalog. If you give it the
coefficients of a polynomial of any degree then it will give you the
roots to any desired number of significant figures. If one or more of
the roots are complex then it will ignore those and give only the real
ones.
Author: Colin Croft
|
|
|
|
|
|
| |
..
|
Root Finding (Advanced) |
| |
This aplet was created by Roso Giuseppe (Beppe) and allows the
user to perform some very advanced matrix operations. He says
"I'm sending an aplet with my build of Newton-Raphson,
bisections and secants
algorithms. A full explanation is supplied in pdf format. In my
algorithms I show every calculus."
Note: The 38G version will probably not become
available.
|
|
 |
|
|
|
| |
.
|
RPN Simulator |
| |
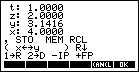 This
program was created by Edward Shore to cleverly simulate Reverse Polish
Notation on the calculator. It's not as flexible as the real
thing but for
anyone wanting to find out why people enthuse over RPN, here's a
chance to try it out.
Note: This is a program NOT an aplet and should be
downloaded from the Program Catalog view not the Aplet view.
Author: Edward Shore <ews773@hotmail.com>
|
|
|
|
| |
.
| Simult 3x3 |
| |
 One of the lacks on the HP has always been a quick and easy
solver of simultaneous linear equations. This fantastic aplet,
written in machine code for speed, fills in this hole perfectly.
Highly
recommended.
Note: On the hp 39g+ you MUST use the
"Wire" option in the RECV menu to download this aplet, not the
"Disk drive" option. When it pops up a window showing
the files, choose "aplet.s". Otherwise the process is normal. On
the hp 39gs/40gs, use the '39/40 USB' option.
Updated 28th Oct. 2003 - The solutions are now stored into
variables X, Y and Z. This means that you can use them in the
HOME view for later calculations, providing you don't over-write
them. For example, using the PLOT screen over-writes X.Author: Michaël De Coninck |
|
|
|
| |
..
.
.
|
Surd Simplifier |
| |
This is a small but very handy program written by a student
who obviously has some interesting ideas. If you enter a surd or
an expression involving surds it will return the simplified
version.
Author: Dale Shelton
Note: It is a program NOT an aplet, which means that you
have to download it into the Program Catalog not the Aplet
Library.
|
|
|
|
|
|
| |
..
.
.
.
|
Ultimate Simplifier |
| |
This is a small program that takes a value you've found and
tries to find an exact value for it, for example a surd or a
fraction of pi or of e. If you've found your answer in Solve and
need an exact value then this may be of use to you. This is a
program not an aplet and should be downloaded to the Program
Catalog.
Author: Alan
Lark.
|
|
|
|
|
|
| |
.
| WindFix |
| |
For those not wanting the full Function 'Plus' aplet (see
above), this is a small program which does the same as the aplet
but takes up less memory and will work with any aplet. For
documentation, download Function 'Plus'. The difference is that
this is a program instead of an aplet and hence is not run
through the VIEWS menu.
More Information
Author: Colin Croft
|
|
|
|
|
|
| |
|
|
| |
The programs below are an excellent
collection of utilities and Notes written by Quin Pendragon, a former year 12
student at Helena College. Some are better than others but most are highly
useful. Quin has grouped his programs into subject areas (for Western
Australian subjects) and if you want to use them then you should download each
ZIP file into its own directory. I have tried some of these but not all
and I make no promises about them working OR giving the correct answers
mathematically. If you have any problems let me know and I'll pass it on to
Quin.
.
Note: Quin has chosen to write
programs rather than ApLets. This means that you need to load them from
the Program Catalogue rather than from the LIB view. Other
than this the process is the same. Programs take up less memory than
ApLets but are a little less convenient to use. If you are thinking of
doing something similar then be warned: I don't put material on my page
without documentation.
| |
| |
| Year 12 Applicable
Mathematics |
| |
A set of small programs written for the year 12 Applicable
Mathematics course in Western Australia. They may be of
interest to other students whose courses contain similar topics.
Information |
|
|
|
|
|
| |
.
| Year 12 Calculus |
| |
A set of small programs written for the year 12 Calculus
course in Western Australia. They may be of interest to
other students whose courses contain similar topics.
Information |
|
|
|
|
|
| |
.
| Chemistry |
| |
A set of small programs written for the Chemistry student in
Western Australia. Most Chemistry courses will overlap
enough for them to be useful to other students.
Information |
|
|
|
|
|
| |
.
| Physics |
| |
A set of small programs for the Physics student in Western
Australia. Most Physics courses will overlap enough for
them to be useful to other students.
Information |
|
|
|
|
|
| |
.
| Games |
| |
A series of small games for the calculator. Because they
are not written in machine code they are not fast and, not being
a game enthusiast, I can't comment on their quality. You
can find information on them, including the controlling keys, here. |
|
|
|
|
|
| |
|
|
| |
|
Supplied along with a worksheet, this aplet encourages the
student to deduce the Chain Rule for themselves via a series of
pre-loaded examples.
This aplet uses chords of diminishing lengths to find the
limiting gradient at a point. A worksheet leads the student into
discovering differentiation. (Used to be called 'A Different
Slant').
This one is just for fun. A series of pre-defined graphs which
look like Christmas trees, including one which is infinitely
detailed near zero. Could be good for a 'rainy day'
exercise.
This aplet is ideal for use when first introducing the
concepts of integration. It uses upper and lower
rectangles to find the areas under supplied curves. A worksheet
then takes the student through the process of deducing the rules
of integration.
Function
Deluxe
This is a copy of the Function aplet with
a vast number of extra features added via an amended VIEWS
menu. It appears to be very useful and I would recommend
checking it out.
An
aplet developed by Quin Pendragon (see 
Another version, written in French by Yves Quemener. It looks
good but I can't evaluate it because there's no documentation at
all and I don't speak French. If anyone would like to compare
the two and let me know which is better...
Another version, also written in French.
The author, Hydreprod, informs me that it uses the F1 function the of the function Aplet.
The user writes the function using the X and Y variables ( for example : f1(x)=1/x+1/y )
and then launches the aplet ('Start 3.d'). After being created, the image is
stored in graphic variable G0 and can then be pasted into a
sketch or used in a program.
This aplet provides simple drill practice for students
learning the laws of indices, with the option of including
negative powers. It presents students with practice
problems in correct mathematical layout and then allows them to
enter the simplified answer. There are a wide variety of styles
of problem. It will then tell them if they are right or wrong,
offering a second chance if needed.
This is a copy of the function aplet with the additional
ability to graph inequalities (linear/non-linear) for F1, F2 and
F3(X). These can be overlaid to show intersections or
unions.
An aplet similar to the Quadratic and Trig Explorers (but not
as fast) which allows the student to explore linear
graphs. The equation of the graph is displayed at the top
left corner of the screen and the student can change the
gradient and y-intercept using the arrow keys. Intercepts
are shown on the screen.
This aplet shows visually the process involved in the Newton-Raphson iteration. It is a useful aid both to teaching
the topic and to illustrating instability based on starting
points.
This aplet illustrates the production of the sine, cosine and
tangent graphs from the unit circle. Recommended.
Given a function, this aplet will produce a slope field based
on it. The user can then move the cursor to a point and draw the
integral function through the field of slopes. This is a
difficult topic to teach well and this aplet is invaluable as an
illustrative tool.
This aplet offers an introduction to the basic idea of
calculus via the minimisation of surface area on a box with
fixed volume. The solution is done via 'trial and adjustment'.
This aplet is basically a copy of the Function aplet with an
additional ability to add a moving tangent line to a
graph. Three predefined functions are available, in
addition to a user defined option. The co-ordinates and
the gradient are displayed at the top left corner of the screen
as the tangent moves along the curve.